Towards Out-of-core ND-Arrays
This work is supported by Continuum Analytics and the XDATA Program as part of the Blaze Project
tl;dr We propose a system for task-centered computation, show an example with out-of-core nd-arrays, and ask for comments.
Note: This post is not user-focused. It is intended for library writers.
Motivation
Recent notebooks (links 1, 2) describe how Blaze handles out-of-core single-dataset tabular computations in the following stages.
- Partition the dataset into chunks
- Apply some computation on each chunk
- Concatenate the results (hopefully smaller)
- Apply another computation into the concatenated result
Steps 2 and 4 require symbolic analysis of what work should be done; Blaze does this well. Steps 1 and 3 are more about coordinating where data goes and when computation executes.
This setup is effective for a broad class of single-dataset tabular computations. It fails for more complex cases. Blaze doesn’t currently have a good target for describing complex inter-block data dependencies. The model for breaking apart data and arranging computations (1 and 3) is too simple.
A good example of a complex case is an nd-array matrix-matrix multiply / dot product / tensor contraction. In this case a blocked approach has a more complex communication pattern. This post is about finding a simple framework that allows us to express these patterns. It’s about finding a replacement for steps 1 and 3 above.
Task Scheduling
The common solution to this problem is to describe the computation as a bipartite directed acyclic graph where nodes are computations and data and edges indicate which pieces of data a computation takes as input and delivers as output.
Many solutions to this problem exist, both theoretical algorithms and implemented software. Forgive me for describing yet-another system.
dask
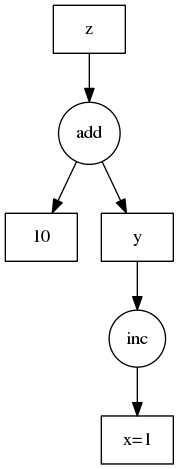
We use a low-tech representation of a task dependency graph. We use a dictionary of key-value pairs where keys are any hashable identifier and values are one of the following:
- A value, like
1 - A tuple containing a function and arguments, like
(inc, 1). This is like an s-expression and should be interpreted as an unevaluatedinc(1) - A tuple containing a function and arguments. Arguments may include other
keys,
(inc, 'my_key')
This is more clear with an example. We show this example on the right.
d = {'x': 1,
'y': (inc, 'x'),
'z': (add, 'y', 10)}
The dask library contains a small
reference implementation to get values associated to keys in this task graph.
>>> import dask
>>> dask.get(d, 'x')
1
>>> dask.get(d, 'y') # Triggers computation
2
>>> dask.get(d, 'z') # Triggers computation
12
In principle this could be executed by a variety of different implementations each with different solutions for distributed computing, caching, etc..
Dask also includes convenience functions to help build this graph.
>>> dask.set(d, 'a', add, args=['x', 'y'])
Although this is mainly to help those who feel uncomfortable putting the parenthesis on the left side of a function call to avoid immediate execution
>>> # d['a'] = add( 'x', 'y') # intend this
>>> d['a'] = (add, 'x', 'y') # but write this to avoid immediate execution
Why low tech?
These “graphs” are just dictionaries of tuples. Notably, we imported dask
after we built our graph. The framework investment is very light.
- Q: Why don’t we build
TaskandDataclasses and construct a Python framework to represent these things formally? - A: Because people have to learn and buy in to that framework and that’s hard to sell. Dictionaries are easier to sell. They’re also easy to translate into other systems. Additionally, I was able to write a reference implementation in a couple dozen lines.
It’s easy to build functions that create dicts like this for various
applications. There is a decent chance that, if you’ve made it this far in
this blogpost, you already understand the spec.
ND-Arrays
I want to encode out-of-core ND-Array algorithms as data. I’ve written a few functions that create dask-style dictionaries to help me describe a decent class of blocked nd-array computations.
The following section is a specific example applying these ideas to the domain of array computing. This is just one application and not core to the idea of task scheduling. The core ideas to task scheduling and the dask implementation have already been covered above.
Getting blocks from an array
First, we break apart a large possibly out-of-core array into blocks. For convenience in these examples we work in in-memory numpy arrays rather than on-disk arrays. Jump to the end if you’d like to see a real OOC dot product on on-disk data.
We make a function ndget to pull out a single block
>>> x = np.arange(24).reshape((4, 6))
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23]])
>>> # Cutting into (2, 3) shaped blocks, get the (0, 0)th block
>>> ndget(x, (2, 3), 0, 0)
array([[0, 1, 2],
[6, 7, 8]])
>>> # Cutting into (2, 3) shaped blocks, get the (1, 0)th block
>>> ndget(x, (2, 3), 1, 0)
array([[12, 13, 14],
[18, 19, 20]])
We now make a function getem that makes a dict that uses this ndget
function to pull out all of the blocks. This creates more keys in our
dictionary, one for each block. We name each key by the key of the array
followed by a block-index.
getem: Given a large possibly out-of-core array and a blocksize, pull apart that array into many small blocks
>>> d = {'X': x} # map the key 'X' to the data x
>>> getem('X', blocksize=(2, 3), shape=(4, 6))
{('X', 0, 0): (ndget, 'X', (2, 3), 0, 0),
('X', 1, 0): (ndget, 'X', (2, 3), 1, 0),
('X', 1, 1): (ndget, 'X', (2, 3), 1, 1),
('X', 0, 1): (ndget, 'X', (2, 3), 0, 1)}
>>> d.update(_) # dump in getem dict
So we have a single original array, x and using getem we describe how to
get many blocks out of x using the function ndget for on each block.
ndgetactually does work on datagetemcreates dask dict that describes on what ndget should operate
We haven’t done work yet. We only do work when we finally call dask.get on
the appropriate key for one of the blocks.
>>> dask.get(d, ('X', 1, 0)) # Get block corresponding to key ('X' ,1, 0)
array([[12, 13, 14],
[18, 19, 20]])
We use numpy.ndarrays for convenience. This would have worked with anything
that supports numpy-style indexing, including out-of-core structures like
h5py.Dataset, tables.Array, or bcolz.carray.
Example: Embarrassingly Parallel Computation
If we have a simple function
def inc(x):
return x + 1
That we want to apply to all blocks of the dataset we could, in principle, add the following to our dictionary.
>>> d.update({('X-plus-1', i, j): (inc, ('X', i, j)) for i in range(2)
for j in range(2)})
>>> dask.get(d, ('X-plus-1', 0, 0))
array([[1, 2, 3],
[7, 8, 9]])
Our use of keys like ('name', i, j) to refer to the i,jth block of an array is
an incidental convention and not intrinsic to dask itself. This use of
tuples as keys should not be confused with the use of tuples in values to
encode unevaluated functions.
Index expressions
A broad class of array computations can be written with index expressions
\(Z*{ij} = X*{ji} \;\;\) – Matrix transpose
\(Z*{ik} = \sum_j X*{ij} Y\_{jk} \;\;\) – Matrix-matrix multiply
Fortunately, the blocked versions of these algorithms look pretty much the
same. To leverage this structure we made the function top for tensor
operations (ideas for a better name welcome). This writes index operations
like the following for blocked transpose:
>>> top(np.transpose, 'Z', 'ji', 'X', 'ij', numblocks={'X': (2, 2)})
{('Z', 0, 0): (numpy.transpose, ('X', 0, 0)),
('Z', 0, 1): (numpy.transpose, ('X', 1, 0)),
('Z', 1, 0): (numpy.transpose, ('X', 0, 1)),
('Z', 1, 1): (numpy.transpose, ('X', 1, 1))}
The first argument np.transpose is the function to apply to each block.
The second and third arguments are the name and index pattern of the output.
The succeeding arguments are the key and index pattern of the inputs. In this
case the index pattern is the reverse. We map the ijth block to the jith
block of the output after we call the function np.transpose.
Finally we have the numblocks keyword arguments that give the block structure
of the inputs. Index structure can be any iterable.
Matrix Multiply
We represent tensor contractions like matrix-matrix multiply with indices that
are repeated in the inputs and missing in the output like the following. In
the following example the index 'j' is a contracted dummy index.
>>> top(..., Z, 'ik', X, 'ij', Y, 'jk', numblocks=...)
In this case the function receives an iterator of blocks of data that iterate
over the dummy index, j. We make such a function to take iterators of square
array blocks, dot product the pairs, and then sum the results. This is the
inner-most loop of a conventional blocked-matrix-matrix multiply algorithm.
def dotmany(A, B):
return sum(map(np.dot, A, B))
By combining this per-block function with top we get an out-of-core dot
product.
>>> top(dotmany, 'Z', 'ik', 'X', 'ij', 'Y', 'jk', numblocks={'X': (2, 2),
'Y': (2, 2)})
{('Z', 0, 0): (dotmany, [('X', 0, 0), ('X', 0, 1)],
[('Y', 0, 0), ('Y', 1, 0)]),
('Z', 0, 1): (dotmany, [('X', 0, 0), ('X', 0, 1)],
[('Y', 0, 1), ('Y', 1, 1)]),
('Z', 1, 0): (dotmany, [('X', 1, 0), ('X', 1, 1)],
[('Y', 0, 0), ('Y', 1, 0)]),
('Z', 1, 1): (dotmany, [('X', 1, 0), ('X', 1, 1)],
[('Y', 0, 1), ('Y', 1, 1)])}
The top function inspects the index structure of the inputs and outputs and
constructs dictionaries that reflect this structure, matching indices between
keys and creating lists of keys over dummy indices like j.
And that was it, we have an out-of-core dot product. Calling dask.get on these keys results in out-of-core execution.
Full example
Here is a tiny proof of concept for an out-of-core dot product. I wouldn’t expect users to write this. I would expect libraries like Blaze to write this.
Create random array on disk
import bcolz
import numpy as np
b = bcolz.carray(np.empty(shape=(0, 1000), dtype='f8'),
rootdir='A.bcolz', chunklen=1000)
for i in range(1000):
b.append(np.random.rand(1000, 1000))
b.flush()
Define computation A.T * A
d = {'A': b}
d.update(getem('A', blocksize=(1000, 1000), shape=b.shape))
# Add A.T into the mix
d.update(top(np.transpose, 'At', 'ij', 'A', 'ji', numblocks={'A': (1000, 1)}))
# Dot product A.T * A
d.update(top(dotmany, 'AtA', 'ik', 'At', 'ij', 'A', 'jk',
numblocks={'A': (1000, 1), 'At': (1, 1000)}))
Do work
>>> dask.get(d, ('AtA', 0, 0))
CPU times: user 2min 57s, sys: 6.59 s, total: 3min 4s
Wall time: 2min 49s
array([[ 334071.93541158, 250297.16968262, 250404.87729587, ...,
250436.85274716, 250330.64262904, 250590.98832611],
[ 250297.16968262, 333451.72293343, 249978.2751824 , ...,
250103.20601281, 250014.96660956, 250251.0146828 ],
[ 250404.87729587, 249978.2751824 , 333279.76376277, ...,
249961.44796719, 250061.8068036 , 250125.80971858],
...,
[ 250436.85274716, 250103.20601281, 249961.44796719, ...,
333444.797894 , 250021.78528189, 250147.12015207],
[ 250330.64262904, 250014.96660956, 250061.8068036 , ...,
250021.78528189, 333240.10323875, 250307.86236815],
[ 250590.98832611, 250251.0146828 , 250125.80971858, ...,
250147.12015207, 250307.86236815, 333467.87105673]])
Three minutes for a 7GB dot product. This runs at about half the FLOPS of a normal in-memory matmul. I’m not sure yet why the discrepancy. Also, this isn’t using an optimized BLAS; we have yet to leverage multiple cores.
This isn’t trivial to write, but it’s not bad either.
Complexity and Usability
This system is not appropriate for users; it’s unPythonic, low-level, and LISP-y. However I believe that something like this would be an appropriate standard for infrastructural libraries. It’s a simple and easy standard for code to target.
Using projects like into and blaze we can build a usable high-level
front-end onto dask for the subproblems of arrays and tables. Blaze could
generate these dictionaries and then hand them off to other systems to execute.
Execution
Using the reference implementation, multithreading, HDF5/BColz, and out-of-core
caching systems like chest I think that we can build a decent out-of-core
ndarray solution that fully leverages a large workstation.
Ideally other people come along and build better execution engines / task schedulers. This might be an appropriate application for IPython parallel.
Help
This could use design and technical feedback. What would encourage community buy-in to a system like this?
blog comments powered by Disqus